Double click to edit
Wiedza matematyczna
Do rozwiązywania zadań z grafiki żółwia potrzebna jest pewna wiedza matematyczna. Przyda się umiejętność wyznaczenia kątów w rysowanych figurach, ustalania wzajemnych proporcji
oraz znajomość twierdzenia Pitagorasa przydatna do określania, między innymi,
długośći przekątnej w kwadracie oraz wysokości w trójkącie równobocznym.
oraz znajomość twierdzenia Pitagorasa przydatna do określania, między innymi,
długośći przekątnej w kwadracie oraz wysokości w trójkącie równobocznym.
Twierdzenie Pitagorasa
PASEK 2
PASEK 6
Przekształcając równanie a2+b2=c2
możemy obliczyć długości
poszczególnych boków
trójkąta prostokątnego:
możemy obliczyć długości
poszczególnych boków
trójkąta prostokątnego:
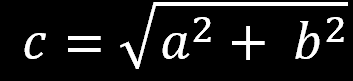
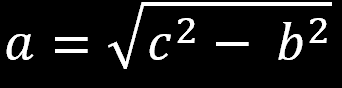
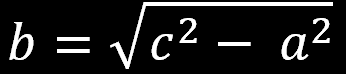
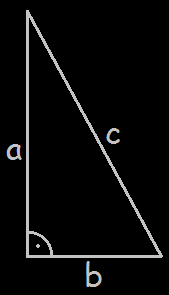
Jeżeli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych
(oznaczonych rysunku obok jako a i b) jest równa
kwadratowci długości przeciwprostokątnej (c), czyli a2+b2=c2
(oznaczonych rysunku obok jako a i b) jest równa
kwadratowci długości przeciwprostokątnej (c), czyli a2+b2=c2
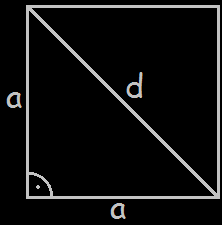
Korzystając z twierdzenia Pitagorasa możemy obliczyć długość przekątnej w kwadracie
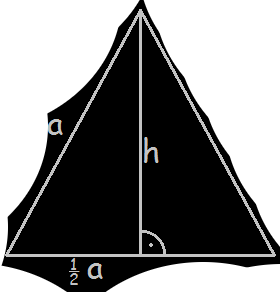
oraz wysokość w trójkącie równobocznym
oraz wysokość w trójkącie równobocznym
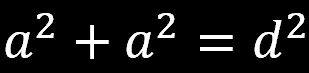
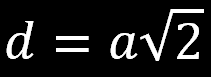
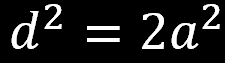
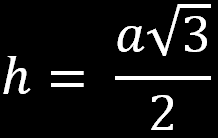
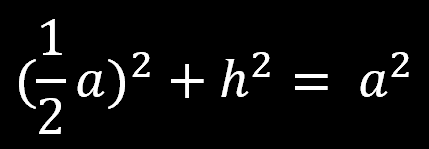
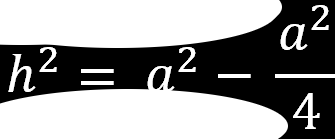
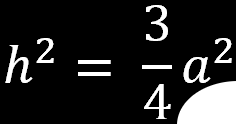
Kwadrat
Kwadrat jest najczęściej wykorzystywaną figurągeometryczną.
W zadaniach stosujemy najczęściej te dwie procedury rysowania kwadratu:
W zadaniach stosujemy najczęściej te dwie procedury rysowania kwadratu:
a) KWADRAT - rysowany w prawo od dolnego lewego narożnika
b) KWADRAT_S - rysowany od środka
b) KWADRAT_S - rysowany od środka
oto KWADRAT :bok
powtórz 4 [np :bok pw 90]
już
powtórz 4 [np :bok pw 90]
już
oto KWADRAT_S :bok
pod ws :bok/2 lw 90 np :bok/2 pw 90 opu
powtórz 4 [np :bok pw 90]
pod pw 90 np :bok/2 lw 90 np :bok/2 opu
już
pod ws :bok/2 lw 90 np :bok/2 pw 90 opu
powtórz 4 [np :bok pw 90]
pod pw 90 np :bok/2 lw 90 np :bok/2 opu
już


Trójkąt równoboczny
W zadaniach wykorzystujemy następujące procedury:
a) TRÓJKĄT
b) Trókąt rysowany od środka - TRÓJKĄT_S
b) Trókąt rysowany od środka - TRÓJKĄT_S
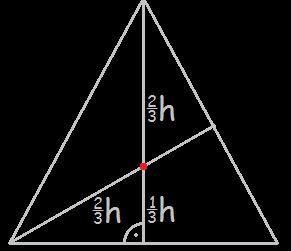
W przypadku procedury TRÓJKĄT_S
za środek trójkąta równobocznego
przyjmujemy punkt równoodległy
od każdego z wierzchołków.
za środek trójkąta równobocznego
przyjmujemy punkt równoodległy
od każdego z wierzchołków.
oto TRÓJKĄT :bok
powtórz 3 [np :bok pw 120]
już
powtórz 3 [np :bok pw 120]
już
oto TRÓJKĄT_S :bok
pod ws :bok*(pwk 3)/6 lw 90 ws :bok/2 opu
powtórz 3 [np :bok pw 120]
pod np :bok/2 pw 90 np :bok*(pwk 3)/6 opu
już
pod ws :bok*(pwk 3)/6 lw 90 ws :bok/2 opu
powtórz 3 [np :bok pw 120]
pod np :bok/2 pw 90 np :bok*(pwk 3)/6 opu
już
Sześciokąt foremny
W zadaniach będziemy wykorzystywać następujące procedury:
a) SZEŚCIOKĄT
b) Sześciokąt rysowany od środka SZEŚCIOKĄT_S
b) Sześciokąt rysowany od środka SZEŚCIOKĄT_S
Warto zauważyć, że sześciokąt foremny składa się
z sześciu trójkątów równobocznych.
z sześciu trójkątów równobocznych.

oto SZEŚCIOKĄT :bok
powtórz 6 [np :bok pw 60]
już
powtórz 6 [np :bok pw 60]
już
oto SZEŚCIOKĄT_S :bok
pod pw 60 ws :bok lw 60 opu
powtórz 6 [np :bok pw 60]
pod pw 60 np :bok lw 60 opu
już
pod pw 60 ws :bok lw 60 opu
powtórz 6 [np :bok pw 60]
pod pw 60 np :bok lw 60 opu
już
Prostokąt
W zadaniach wykorzystamy następujące procedury:
a) PROSTOKĄT
b) Prostokąt rysowany od środka PROSTOKĄT_S
b) Prostokąt rysowany od środka PROSTOKĄT_S


oto PROSTOKĄT :a :b
powtórz 2 [np :a pw 90 np :b pw 90]
już
powtórz 2 [np :a pw 90 np :b pw 90]
już
oto PROSTOKĄT :a :b
pod ws :a/2 lw 90 np :b/2 pw 90 opu
powtórz 2 [np :a pw 90 np :b pw 90]
pod pw 90 np :b/2 lw 90 np :a/2 opu
już
pod ws :a/2 lw 90 np :b/2 pw 90 opu
powtórz 2 [np :a pw 90 np :b pw 90]
pod pw 90 np :b/2 lw 90 np :a/2 opu
już
Okrąg
W zadaniach wykorzystamy jedynie polecenie OKRĄG
Przykład:
okrąg 100
okrąg 100